许多实际的优化问题都有相互冲突的目标,这应该通过多标准优化(MCO)来解决,即通过确定最佳妥协集,帕累托集(PS),以及它在参数空间中的图像(PSPS)。在之前关于低维MCO问题的研究中,我们已经发现了PS和PSPS的特征拓扑特征,它们依赖于参数空间M和目标空间N的维数,例如,\(M=2\)和\(N=3\)产生具有针状扩展的三角形。到目前为止,这些拓扑特征的原因尚不清楚。在这里,我们证明,如果MCO的所有目标函数满足两个条件,则它们是预期的:(a)它们可以用二次函数逼近;(b)在函数的最小值处计算的Hessian矩阵的一个特征值与其他特征值相比较小。满足条件(a)和(b)的目标函数具有类谷拓扑,其中谷位于最低特征值对应的特征向量方向。PSPS可以通过从目标函数的最小值开始,沿着谷值,并将所有目标函数的这些线组合起来来估计。通过对目标函数的求值,得到目标函数的PS。我们认为条件(a)和(b)在许多实际问题中都是满足的,并讨论了分子建模中的一个例子。对这些MCO问题特征的更好理解为设计方法快速找到其PS和PSPS的估计开辟了道路。
在许多实际应用中,即在工程中,会遇到目标冲突的优化问题;而多准则优化(MCO)是解决这些问题的合适方法。在MCO中,帕累托集合(PS)是确定的,它是目标之间的最佳可能妥协集合(帕累托2014)。对于PS上的任何一点,一个目标的改善只能以至少一个其他目标的下降为代价;因此,PS代表了MCO问题的最优解。有关详细的数学讨论,请参阅参考文献Ehrgott(2005)。在实际的MCO问题中,通常只能实现一个解,该解应从PS中选择。在MCO中,不仅确定了PS,还确定了其在参数空间中的图像(PSPS)。在PS上选择一个点后,PSPS显示需要哪些参数才能到达该点。确定PS远非微不足道,因为从实际的角度来看,参数空间的暴力枚举通常是不可行的。因此,已经开发了确定PS的专用方法,例如,ologist等人(2010),Hernandez(2012),但这些方法通常仍然需要对目标函数进行大量评估。本文研究了低维PS的拓扑结构,因为它们在许多实际问题中都遇到过。这些结果可以快速估计这些情况下的PS。
MCO已应用于许多工程领域,例如能源系统的设计(Shirazi et al. 2014;Najafi et al. 2014),半导体(Ganesan et al. 2015)和化学工艺(Clark and Westerberg 1983;Bhaskar et al. 2000;Rangaiah and Petriciolet 2013;H?ller等人,2019;von Kurnatowski et al. 2017;Bortz et al. 2014)。在热力学领域,仅举一个例子,MCO之前已被用于模拟纯化合物和混合物(Kulkarni et al. 2020;St?bener等,2014,2016;Werth et al. 2015;Kohns等人,2016),状态方程(Rehner和Gross 2020;格雷厄姆2020年;Forte et al. 2017)和超额吉布斯能量模型(Forte et al. 2020)。在这样的应用中,目标的数量N和参数的数量M通常都很低,两个数字的典型值都低于5。然而,如果目标函数的评估是昂贵的,例如在分子模型的开发中,那么即使对于这种低维的MCO问题,PS的确定也可能成为一个严重的问题。
在我们之前关于热力学中MCO的研究中(Kulkarni et al. 2020;St?bener et al. 2014;Kohns et al. 2016),我们已经观察到PSPS和PS的特征拓扑,它们依赖于N和M的数字,但不依赖于所研究的具体问题。图1显示了某些情况下这些拓扑的示意图。
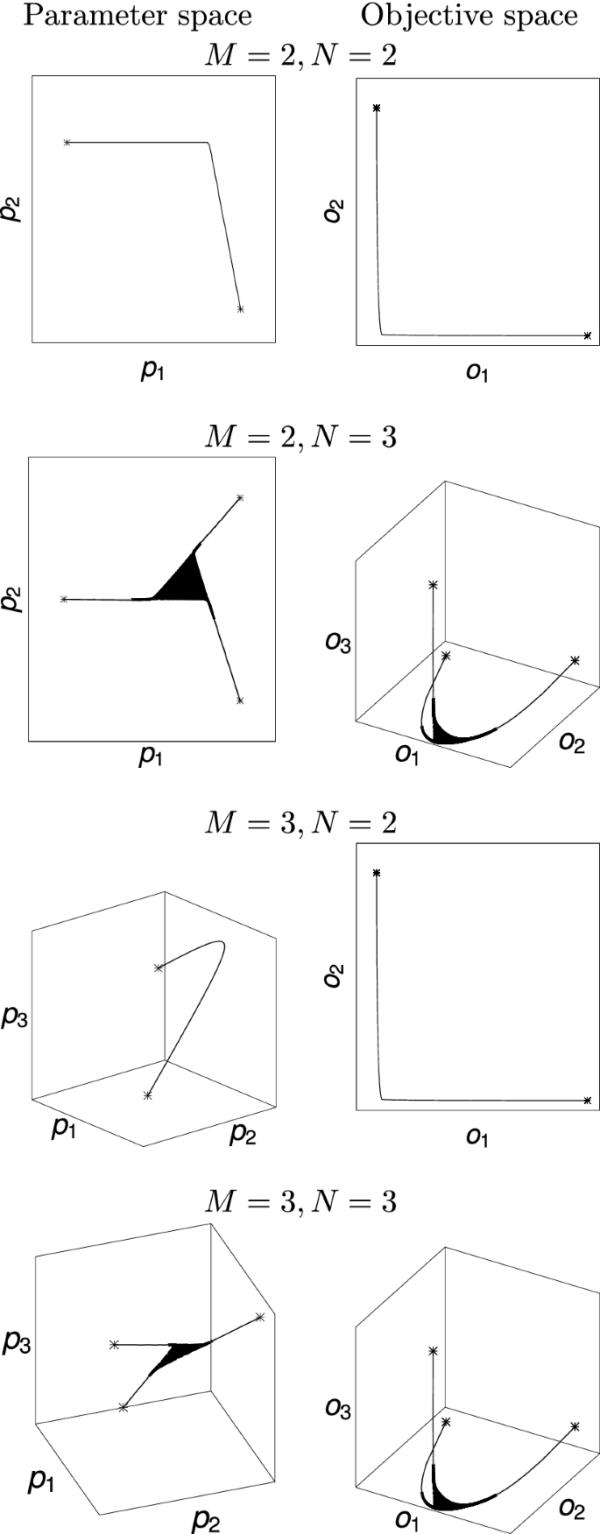
本小组在之前的研究中观察到的具有N个目标和M个参数的低维MCO问题的目标空间中典型Pareto集拓扑(PS,右图)的草图及其在参数空间(PSPS,左图)中的图片(Kulkarni et al. 2020;St?bener et al. 2014;Kohns et al. 2016;Forte et al. 2020)。星号表示极端妥协,即N个独立目标函数的全局最小值
因为,PS和PSPS都有两个不同的分支,它们几乎都是直线。靠近分支交叉点的区域是所谓的帕累托膝盖区域,该区域的两个目标值通常都较低,而远离帕累托膝盖区域的分支则一个目标值较高,另一个目标值较低。因为,PSPS在中心显示出三角形,从顶点延伸出针状,然而,这并不总是被观察到。在这种情况下,中心三角形区域是帕累托膝。
之前已经证明了这一点(Kulkarni et al. 2020;St?bener et al. 2014;Kohns et al. 2016),这些特征拓扑与MCO问题的单个目标函数的性质密切相关。然而,这种关系的内部运作尚未被揭示,这些特征拓扑发生的条件仍然未知。因此,本工作的出发点是希望澄清这些问题。该方法背后的中心假设是,如果单个目标函数的拓扑满足一定的要求,则可以观察到特征拓扑特征,目的是阐明相应的条件。
奥古斯托等人(2014)发表的研究结果被证明是解决这一挑战的关键。Augusto等人(2014)在所有目标函数都是二次函数的情况下,推导出M和N任意数的PSPS的解析表达式。如果满足一定条件,可以从它们的结果中得到图1所示的拓扑。基本上,图1中的线对应于各个目标函数轮廓中的谷值。在数学上,山谷可以与单个目标函数的特征值和特征向量在其最小值处相关(图1中的叉)。由此可以推导出数学条件,如果满足这些条件,则会导致特征拓扑的出现。
在许多实际MCO问题的目标函数中都发现了这种类谷拓扑。例如,我们在之前所有热力学领域的MCO研究中都观察到了这样的拓扑结构,与所使用的热力学模型类型无关,即分子模型(Kulkarni et al. 2020;St?bener et al. 2014;Kohns et al. 2016),状态方程(Forte et al. 2018),以及吉布斯过剩能量模型(Forte et al. 2020)。此外,在其他各个领域的MCO问题中,例如工艺设计(Bortz et al. 2014, 2017;Burger等人,2014),能源系统工程(Chiu等人,2019),以及定量光谱学(Matviychuk等人,2020),发现PS表明目标函数拓扑结构的山谷状结构。我们这里指的是PS中所谓的“帕累托膝”的存在(Branke et al. 2004),这可能被解释为拓扑中相互相交的谷的结果。如果这些山谷是陡峭的,那么产生的帕累托弯将是尖锐的。
因此,我们有充分的理由相信,我们在目前的工作中所研究的不仅仅是一些特殊的情况,而是一个具有高度实际意义的问题。在我们的研究中获得的见解不仅解释了文献中的经验观察(例如关于帕累托膝),它们也可以用于设计确定PS和实际问题中的PSPS的新方法。我们还详细说明了这里研究的有趣的和实际相关的行为类型必须预期的条件。
为了说明我们的发现,我们讨论了一个实际的MCO问题:水分子模型的发展,其目的是很好地描述不同的热力学性质,即蒸汽压力和液体密度。目标是相互冲突的,因为考虑的水模型类别(这是最常见的一种)相当简单,因此并非所有水的属性都可以同时以高精度建模。因此,必须做出妥协,并且非常希望知道PS,这是最佳妥协的集合。我们表明,对于这个MCO问题,出现了类似山谷的拓扑结构,并且满足了表征它们的数学条件。我们还通过实例讨论了如何在分析单个目标函数的基础上,将本研究的见解用于估计MCO问题的帕累托集。我们注意到,我们在这里研究的MCO问题既不包含目标约束,也不包含参数约束。考虑增加限制的影响超出了本研究的范围,特别是因为它需要对不同类型的限制进行个别考虑(例如分别对公营部门和公营部门的限制)。
本文的组织如下:第2节给出了二次目标函数情况下Pareto集合性质的数学分析,包括基于单个目标函数的性质构造这些集合的估计的讨论。在第3节中,我们讨论如何将这些发现应用于目标函数不是二次函数但可以用二次函数近似的系统。然后通过第4节中的两类例子来说明结果:第一类是对具有合成二次目标函数的系统的研究,第二类是来自热力学的实际MCO问题,即水分子模型的优化。最后,在第五节中得出结论。
一般情况下,m维参数空间中的二次目标函数可以表示为
(1)式中,N为目标空间的维数。向量是参数空间中的一个点,表示的坐标的最小值,是的黑森矩阵。黑森矩阵是一个对称矩阵,因此。
Augusto等人(2014)描述了一种分析方法,用于确定包含由Eq.(1)描述的任意数量的二次目标函数的MCO的PS。附录中描述了适用于任何M和N的完整方法。在这里,我们用一个简单而生动的案例来说明。
设两个目标函数为和,它们的Hessian矩阵为和,它们的最小值为和。可以写成
(2)在那里,。Hessian矩阵是对称的,因此两个非对角元素相等,因此。
原则上,黑森量以及相应的最小值都是任意的。然而,在不丧失一般性的情况下,可以应用坐标变换使(i)位于原点,(ii)的特征向量平行于坐标轴,从而使的非对角线元素消失。此外,为了本讨论的目的,将的特征值之一缩放为1,这不会影响目标函数的拓扑结构。表示另一个特征值,可以写成
(3)改变参数会产生不同的特征值比率。如果两者之一,则得到的是一个谷状拓扑结构。我们将讨论前一种情况,其中山谷在-方向上。
对于两个二次目标函数,根据Augusto et al.(2014)(论文Eq. (27)), PSPS上的任意一点都可以计算如下:
(4) (5)其中,和分别为目标函数和所对应的权值。每个权重的选择都给出了PSPS的一个唯一点,因此Eq.(4)作为函数的评估产生了整个PSPS。然后通过对目标函数和的所有值求出PS。当,该点接近(最小值的坐标),当,该点接近(最小值的坐标)。
在本节中,奥古斯托等人(2014)的结果被用于分析PSPS的拓扑结构,因此,也用于分析PS。为了简单明了,我们继续讨论这个案例,但强调该论点可以推广,如附录所示。
将式(4)重新排列得到:
(6)其中为维数的单位矩阵。
让我们考虑在的附近的一个点,这样。对式(6)中括号内的第一项进行泰勒级数展开式,得到如下近似:
(7)在下面,我们只保留前一项,即:
(8)替换和矩阵的值,得到:
(9)注意,在坐标变换中,的最小值被移到原点,成为对角矩阵,而的最小值一般在其他位置,不是对角矩阵,即。式(9)直接表明,对于时,PSPS逼近原点,即最小值的坐标。
若,Eq.(9)可近似为:
(10)因此,对于的-分量较小,即最小值附近的PSPS靠近-轴。
的特征值为1和,属于特征值1的特征向量是-方向上的向量。因此,Eq.(10)可以解释为:,的最小值与的较小特征值对应的特征向量定义了PSPS在的最小值附近的线性逼近。在空间中对这一发现的几何解释是,对于的最小值位于沿-方向(特征向量对应于特征值1的方向)的山谷底部。PSPS与线性近似的偏差随着与最小值的距离增加(随着增加)和特征值的比例降低而增加。同样的参数也可以应用于。
上述情况下讨论的发现可以推广到M和n的任意值。对于每个目标,可以进行上述分析。如果定义(见Eq.(1))的对角线Hessian矩阵的一个特征值远小于所有其他特征值,则的最小值与该特征值对应的特征向量在最小值附近定义了PSPS的线性近似。一般情况下的相应方程在附录中给出。
我们现在考虑二次目标函数的情况,并假设对于每个目标函数,一个Hessian矩阵的特征值比其他特征值小得多,即目标函数具有类似山谷的拓扑结构。从2.3节可知,仅考虑单个目标函数的谷值即可得到最小值附近MCO问题的Pareto集的估计。我们描述了实现这一目标的两种替代方法。
(a)线性近似线性近似包括对所有目标执行的下列三个步骤:
- (1)
求的最小值。
- (2)
找出属于矩阵最小特征值的特征向量。
- (3)
将1)和2)的结果结合起来,得到PSPS附近的线性近似。
这个过程产生N条直线,这些直线可以组合起来得到PSPS的估计。由此,通过评价MCO问题在PSPS上各点的目标函数,可以找到PSPS。这些单独的线必须结合起来形成PSPS的估计,这取决于M和N。
我们将参考图1来讨论这个问题。让我们考虑第一种情况:有两条线通常会相交。目标空间中的交点称为帕累托拐点。这里给出的论点解释了为什么经常发现非常尖锐的帕累托膝盖。不是所有的线都属于PSPS,而只是它们各自在极小值和帕累托拐点之间的部分。
对于和,二维参数空间中有三条线。这三条线不仅属于PSPS,它们之间的三角形区域也属于PSPS(见图1)。该三角形区域在目标空间中的图像对应于Pareto膝部。我们将把这个连接这些线的区域(包括骶椎和骶椎)称为帕累托膝区。
对于这里考虑的情况(,),PSPS中线之间的面积通常是三角形的,很容易构造。在其他情况下,定义这一领域并不那么简单;例如,对于和,通常有三条线不会相交。关于如何从直线的知识中构造帕累托膝区域的一般理论不属于本研究的范围。直观地说,帕累托膝区域应该是在直线彼此接近的地方找到的,而如何构造它的解决方案将取决于直线接近区域中PSPS的线性逼近的质量。
PSPS的线性逼近只有在极小值附近才有效,而在远离极小值的地方会出现偏差。这些偏差的大小取决于问题的细节,包括不同最小值之间的距离。通过考虑上面提到的泰勒级数展开中的高阶项,有可能得到更好的预测,但这需要知道目标函数的导数高达2阶以上,这在实际问题中可能难以获得。目标函数的谷状拓扑的思想使我们能够设计一种不同的策略,在下面称为谷近似。
(b)谷值近似
谷值近似是线性近似的一种修改,其中上面所示方案中的步骤2被另一种方案所取代,用于寻找从目标函数的最小值开始的线。其中一个特征值比其他特征值小得多的目标函数的几何图是一个类似山谷的拓扑结构。山谷的最低点是的最小值,位于。使用上述a)项下描述的方法,首先在的附近通过线性近似很好地逼近了谷值。然而,随着距离的增加,谷值与线性近似之间将出现偏差。我们建议使用山谷的底线作为PSPS的近似值,而不是使用线性近似值。我们不试图给出一个正式的证明,证明这是对线性近似的改进,但将在下面讨论一些例子,以证实相应的期望。
摘要
1 介绍
2 具有二次目标函数的MCO
3.非二次MCO问题的应用
4 例子
5 结论
参考文献
致谢
作者信息
道德声明
附录
搜索
导航
#####
图1所示的拓扑结构是在化工实际的MCO问题中观察到的,它与前一节关于二次目标函数的理论完全一致。特别是,该理论解释了图1所示的不同情况的发生。因为,只有当目标函数的极小值位于帕累托膝区域之外时,才会发现PSPS的针状扩展。
这表明,对于潜在的MCO问题中的目标函数,以下是成立的:
- (i)
可以用二次函数合理地逼近。
- (2)
的Hessian矩阵的一个特征值,在最小值处的值比另一个特征值小得多。
如果满足这些条件,预计(a)线性近似以及(b)谷值近似可以用于获得PSPS的估计,并相应地获得PS的估计,如第2.4节所述。此外,对于真正的MCO问题,还有一个进一步的选择:
(c)二次近似
在第一步中,对于每个目标函数,围绕其最小值构造二次逼近。然后,将Augusto et al.(2014)的方法应用于这些二次函数中的每一个,从而获得PSPS的估计。
在最小值附近,二次逼近得到与线性逼近相同的结果,但在帕累托拐点区域,它可能严重偏离线性逼近。此外,线性近似和谷值近似只能得到曲线,而二次近似可以得到更高维度的目标,这在Pareto膝部区域是很重要的。
在本节中,我们考虑二维参数空间中由Eq.(2)定义的合成二次目标函数,即。下面定义了三个不同的二次目标函数,和。我们将考虑一个二维目标空间的例子,即只使用两个目标和,以及第二个三维目标空间的例子,即使用所有三个目标和。
如2.2节所述,选择目标函数的最小值为原点,其特征向量平行于坐标轴,两个特征值为1和。因此,是一个对角矩阵,其对角元素为1和。另外两个目标函数,和,是通过围绕原点旋转并将其平移不同的量来获得的,这样最小值就被移动了。由旋转并定位其最小值得到,由旋转并定位其最小值得到。因此,特征值的比率对于所有三个目标是相同的。为所有目标函数选择相同的特征值比率并不是当前分析有效的必要条件;这样做只是为了方便。
两种不同的特征值比率,即10和100,用于评估PSPS和PS的线性近似和谷值近似的准确性(参见第2.4节)。使用Augusto et al.(2014)的方法计算精确解。对于,山谷状景观比对于“更陡峭”。图2示出了三个目标函数、、和。
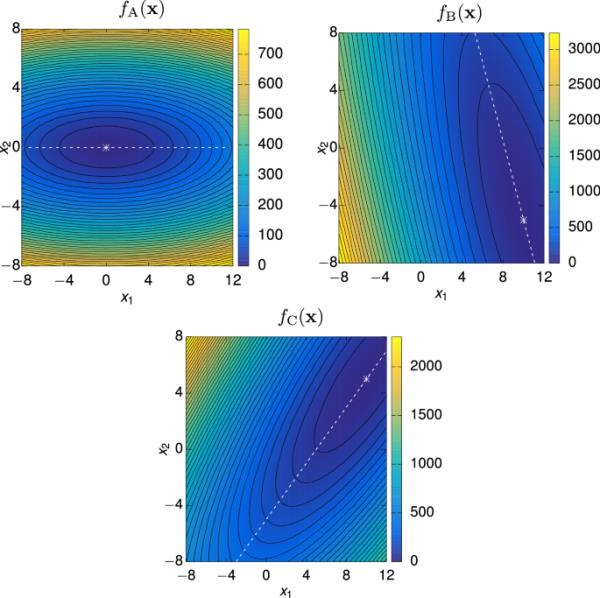
本文研究了三种综合二次目标函数的等值线图。白色星形表示函数的全局最小值,而白色虚线表示穿过最小值的山谷(最低上升路径)
图3给出了考虑两个目标和时MCO的Pareto集合。图中左侧为PSPS,右侧为PSPS。此外,在参数空间中,给出了各个函数的谷值及其极小值(类似于图2),以供参考。
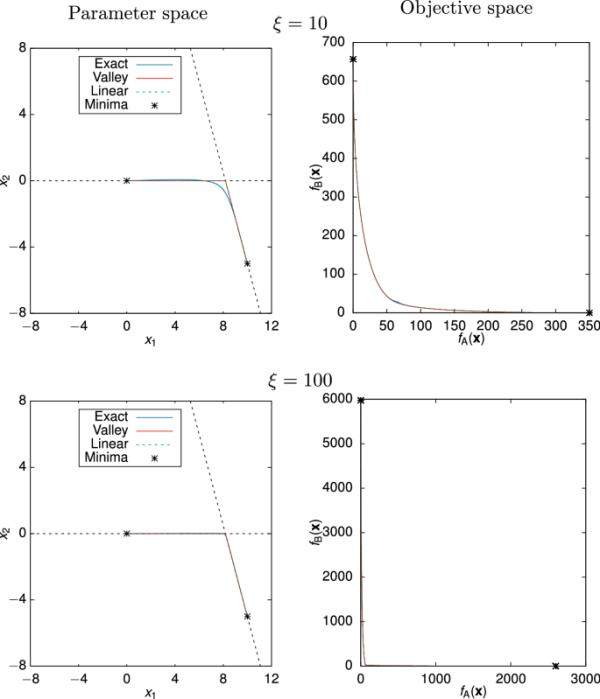
具有两个合成二次目标函数和的MCO的Pareto集。上排:,下排:。左:参数空间(PSPS),右:目标空间(PS)。蓝线:精确解,红线:谷值近似,绿色虚线:线性近似(见第2.4节),黑色虚线:单个函数的谷值。图中的星号表示单个目标函数的全局最小值。谷近似和线性近似在这里是完全相同的
对于合成二次函数,谷是沿着特征向量的直线,这些特征向量对应于目标函数的Hessians的较小特征值。因此,谷值近似(红线)和线性近似(绿色虚线)彼此重合。
对于,除了帕累托膝区域外,PSPS是精确的近似。然而,即使是该区域的差异也很难在PS中显示出来,这是非常近似的。正如预期的那样,近似值甚至更好,对于PSPS和PS,近似值和精确解之间的差异基本上可以忽略不计。
图4给出了所有三个目标、和的合成二次目标函数的帕累托集。再一次,特征值和的两个比值被考虑。对于上面讨论的具有两个目标的情况,PS可以很好地近似于两者。因此,为简洁起见,我们仅在图4中显示PSPS的结果。
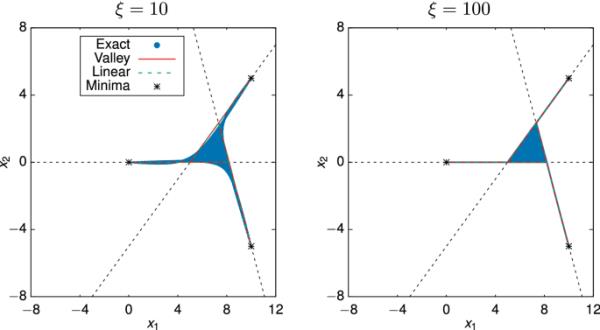
具有三个综合二次目标函数的MCO的PSPS,和。左:,右:。蓝色:精确解,红色:谷值近似,绿色:线性近似,黑色虚线:单个函数的谷值。图中的星号表示单个目标函数的全局最小值。谷近似和线性近似在这里是完全相同的
因为,近似在极小值附近工作得很好,而在帕累托膝区域,可以观察到偏差。因为,这些偏差基本上消失了,导致PSPS几乎完美的近似值。
作为应用在本工作中发展的估计帕累托集的概念的一个实际例子,我们现在讨论热力学中的一个MCO问题,即水分子模型的参数化。因此,我们选择了一个流行的水模型,即所谓的SPC/E模型(Berendsen et al. 1987)作为起点。将MCO应用于流体分子模型开发的问题是,目标函数的评估在计算上非常昂贵,因为它们通常需要在每个迭代步骤中在许多状态点进行分子模拟。我们在这里通过使用所谓的简化单元方法(下文将对此进行解释)以及我们小组之前研究的SPC/E模型的模拟数据(Kulkarni et al. 2020)来规避这个问题。这使我们能够在不进行额外的分子模拟的情况下进行分析。在我们研究的MCO问题中,有三个目标函数用于测量分子模型结果(Kulkarni et al. 2020)与实验数据(Lemmon et al. 2018)之间的差异;Wagner and Pru? 2002)对水的三个重要热力学性质:饱和液体密度()、蒸汽压力()和汽化焓()。相应目标函数的定义,和采用了我们之前的工作(Kulkarni et al. 2020),并纳入了附录。
这里使用了简化单元法(Merker et al. 2012)来获得参数与目标之间的关系。SPC/E模型有5个参数,为了能够应用简化单元法,我们只使用其中的2个参数作为变量()。这是Lennard-Jones尺寸参数和Lennard-Jones能量参数。当和变化时,其他模型参数按规定的方式变化。细节在Merker等人(2012)中给出,对目前的讨论不重要。我们在这里提到这一点只是为了强调,如果在MCO中使用所有参数,那么进一步的改进是可能的,出于计算原因,我们在这里没有这样做,这也便于讨论。如果原始模型(此处为SPC/E)的仿真结果可用,则简化单元法可以得到仿真结果与参数和之间的关系的解析表达式。由此,可以计算出MCO问题的目标、和。我们建议读者参阅原始参考文献Merker et al.(2012),了解有关简化单元方法的更多细节。
三个目标的等值线图,和作为参数和的函数如图5所示。两者都显示了全局极小值以及经过极小值的谷值。在这里,通过选择沿平行于坐标轴的横截面的单个目标的最低值来估计谷值。注意,这并不取决于这里。因此,该物镜的等高线平行于-轴。因此,对于这个目标没有明显的最小值,相反,最小值“分布”在平行于-轴的整条线上,即一条常数线。
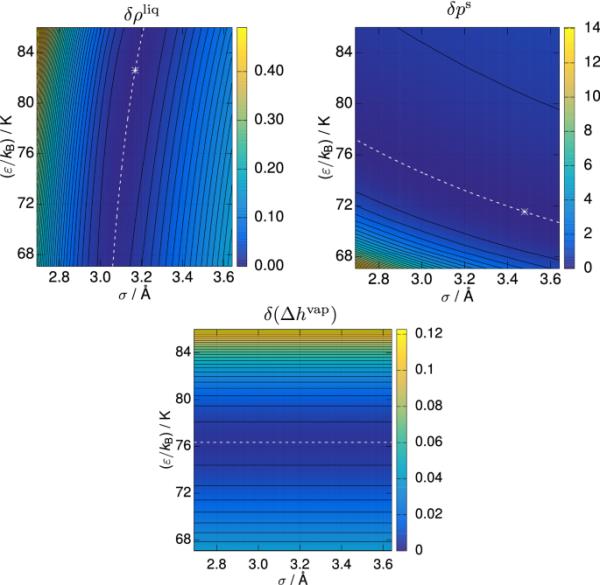
SPC/E水模型优化的三个目标函数等值线图。目标,和分别表示SPC/E的模拟结果与饱和液体密度,蒸汽压和汽化焓的实验数据之间的偏差。白色的星星表示函数的最小值,而白色的虚线表示通过最小值的山谷(最低上升的路径)。没有明确的最小值,因为这个目标不依赖于
由于物镜和参数之间的解析关系是可用的,因此可以在各自的最小值处计算它们的二阶导数。由此可以计算出Hessian矩阵,并得到目标函数的二次逼近。此外,计算了单个目标最小值时的黑森特征值,如表1所示。特征值的比率明显大于合成二次函数的比率,参见第4.1节。
对于此例中的MCO,与合成二次目标函数类似,首先只考虑两个目标,即和,因此。在第二步中,考虑了三个目标,和。对于这两种情况,将PSPS和第3节中给出的三种方法(线性近似、谷值近似和二次近似)得到的PS与精确Pareto集进行比较。后者是通过在窄间距参数网格上对目标函数的数字进行暴力枚举来计算的,然后选择不占主导地位的点。
图6给出了针对该案例的PSPS(左)和PS(右)获得的结果。此外,还提供了PS的帕累托膝盖区域的放大。这三种近似与精确的帕累托集一起显示。此外,给出了两个目标函数的谷值的底线和相应的最小值。
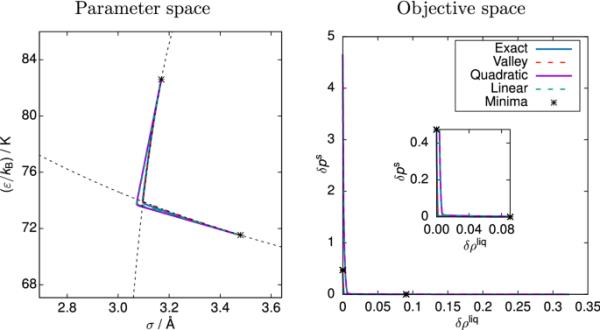
具有和两个目标函数的SPC/E水模型的MCO的Pareto集合。左:参数空间(PSPS),右:客观空间(PS)以及帕累托膝关节周围PS的放大视图。蓝色:精确解,红色:山谷近似,紫色:二次近似,绿色:Pareto集的线性近似。此外,谷值(见图5)以黑色虚线表示,以供参考。星号表示单个目标函数的全局最小值。帕累托集的精确解和谷值逼近是一致的,帕累托集的二次逼近和线性逼近也是一致的
谷值近似与帕累托集几乎完全匹配。由于目标函数不再是严格的二次函数,线性近似偏离了山谷的底线,这是稍微非线性的。线性近似和二次近似显示几乎没有差异,即使在帕累托膝区域,这可以理解为具有尖锐和深谷的单个目标函数的拓扑结构的结果,因此,作为特征值广泛传播的结果。然而,这两个重合的近似值虽然仍然给出了相当的结果,但显然不如(几乎完美的)谷值近似值准确。
图7给出了针对该案例的PSPS(左)和PS(右)获得的结果。如图6所示,将三种近似的结果与精确解进行比较。然而,现在有三个目标函数,因此有三个谷值,其中只有两个具有最小值,原因如上所述。
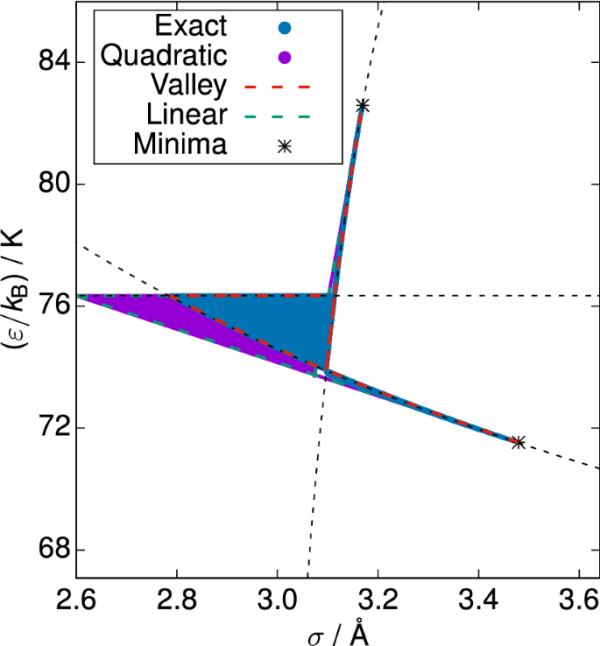
具有三个目标函数的SPC/E水模型MCO的PSPS,和。蓝色:精确解,红色:山谷近似,紫色:二次近似,绿色:线性近似。星号表示单个目标函数的全局最小值。此外,谷值(见图5)以黑色虚线表示,以供参考
在这种情况下,一个三角形的帕累托膝部区域有两个扩展,这就是这里的情况。这两个扩展在两个极小值处结束,这两个极小值位于帕累托膝区域之外。这种拓扑不仅存在于Pareto集的蛮力评估中,而且存在于所有考虑的近似方法中。二次逼近法得到三角形曲面和扩展,而其他两种方法只得到三条相交线,但由此可以很容易地构造包含两个扩展的三角形帕累托膝区域。至于谷值法的预测几乎是完美的,至于二次逼近和线性逼近的结果之间的差异可以忽略不计。再说一遍,这些预测不如谷值近似准确。
综上所述的算例结果表明,谷值近似在实际的MCO问题中是一种准确而有用的近似。
在以往对低维MCO问题的研究中,我们发现Pareto集合及其在参数空间中的图像具有与单个目标函数的拓扑密切相关的特殊拓扑,它们的最小值通常位于一个深而陡的山谷的最低点。这样的结构在数学上的特点是,目标函数的黑森特征值中的一个在其最小值时比其他特征值小得多,这似乎是许多工程问题的情况。这一发现可用于估计MCO问题的帕累托集:单个目标函数的极小值是MCO问题的极端折衷,因此属于帕累托集。在上面描述的情况下,从最小值开始,沿着山谷可以找到更多的帕累托集点。我们称之为谷值近似。所谓的帕累托膝区,通常是最有趣的妥协所在的区域,是在山谷交汇或至少彼此接近的地方发现的。本文首先对具有二次目标函数的MCO问题进行讨论,其中Pareto集可以使用Augusto等人(2014)的方法解析确定。然后,将分析扩展到具有非二次目标函数的MCO问题,但需要具有上述拓扑结构。讨论了确定这些MCO问题的Pareto集的三种方案,其中谷值近似的结果最好。因此,这些结果不仅解释了之前观察到的帕累托集的特殊拓扑结构,而且还可以用来构造帕累托集的近似。
目前的工作遗留的问题包括:(a)对低维实际MCO问题的更多例子的分析。我们的假设是,将会发现许多具有上述奇特拓扑结构的结构。对为什么这类问题如此普遍做出一般性陈述也会很有趣。(b)目前估计帕累托集的方法是基于寻找从极端妥协开始的帕累托集的分支。当不遵循简单的几何考虑(如交点)时,如何找出这些分支在帕累托集合中的连接方式,这个问题基本上没有解决。这里的二次逼近方法,其中所有的目标函数都是围绕其各自的最小值用二次函数逼近,这是在本工作中提出的,可能是有用的,因为它不仅产生分支,而且产生它们的联系。最后,新方法应该在一个健壮和高效的程序包中实现。
下载原文档:https://link.springer.com/content/pdf/10.1007/s11081-022-09746-z.pdf
本文来自作者[彬景]投稿,不代表文学号立场,如若转载,请注明出处:https://8ucq.com/wenxuehao/12155.html


评论列表(4条)
我是文学号的签约作者“彬景”!
希望本篇文章《低维实际多准则优化问题中帕累托集的规律:分析、解释与开发》能对你有所帮助!
本站[文学号]内容主要涵盖:文学号, 名著深析, 创作秘笈, 经典文脉, 诗词鉴赏, 作家故事, 每日文萃, 写作指南, 文本细读, 文学灯塔, 经典重释
本文概览:许多实际的优化问题都有相互冲突的目标,这应该通过多标准优化(MCO)来解决,即通过确定最佳妥协集,帕累托集(PS),以...